Frequently Asked Questions

info

The following FAQ will continue to be updated as the Alphabill platform evolves. Currently, this FAQ is mainly focused on technical questions about the Alphabill platform. If you have a more general question or a question that is not answered here, join the Alphabill Discord server and post your question to the #ask-us-anything channel.

Technical Overview

What's new and why should I care?

Historically, all blockchains have been designed using UTXOs or accounts as transaction units. The implication is that assets (tokens or contracts) are inter-connected—every transaction by definition involves at least two units. These choices severely limit the achievement of performance goals. Either the chain gets congested or additional layers, such as rollups or federated consensus instances are introduced, which introduce compromises in security, performance, settlement finality, etc.

Alphabill is the first blockchain where all assets (tokens or contracts) are independent—there are no cross-dependencies between assets to check during execution and every transaction updates a single unit. This allows for perfect parallelism—all assets can be independently updated and verified, and the global state can be managed by many machines operating in parallel.

This allows us to build a permissionless decentralized blockchain that provides deterministic finality and practical unbounded throughput—there are no cross-dependencies that require a global ordering of transactions to achieve deterministic execution. The data model has been tested at 2M token transfers per second with single second finality using 100 shards operating in parallel. Scaling to 20M token transfers per second requires only more machines, without any impact on settlement finality, that is, the network has linear scale.

Perfect parallelism introduces new classes of use cases that have not been possible before. As the tokens can be independently verified, they can also be extracted and verified off-chain, even off-line. The figure below illustrates parallelization of production and verification.

The approach we have taken has two important implications: real-world use cases and scaling decentralization.

Real-world use cases

The first implication is that tokens are portable, can move across the Internet and be used in the real world—that is, everything from tokenized cash, tokenized session cookies and more generally tokenized data—all data on the Internet can be tokenized and verified without reliance on centralized authorities. Tokens can be verified inside any application development platform—anything from decentralized smart contract platforms or centralized legacy applications. Example of a token portability is shown below.

Scaling decentralization

The second implication is that the parallelization makes it possible to scale the blockchain while maintaining decentralization.

Quoting Vitalik from his blog post on scaling blockchains while maintaining decentralization:

"For a blockchain to be decentralized, it's crucially important for regular users to be able to run a node, and to have a culture where running nodes is a common activity."

With Alphabill, due to parallel decomposition we can change this statement to:

"For a blockchain to be decentralized, it's crucially important for regular users to be able to independently verify their assets, and to have a culture where verifying assets is a common activity."

The analogy with physical cash is relevant. When I give you a 20 USD note, you just check the validity of that note. You don't need to run the entire economy on your mobile device and check every other transaction in history to be sure that your 20 USD note is valid.

One way to scale blockchains is centralization, such as Solana and SUI with high-powered computers as nodes (one shardable, the other not). Another way is decomposition, that is, efficient independent verification of assets. In a sense this is in line with Vitalik's vision except that the work of a "node" can be shared amongst the crowd.

Why has no one used bills as transaction units before?

Bitcoin started with UTXOs and then Ethereum introduced accounts, with the thinking like "let’s build a great thing and then make it scale later". There hasn't been an alternative, and the community has lacked a mathematical formalism or language to understand the choices available and their implications. We spent several years understanding the architectural choices before selecting bills as transaction units.

This paper is the result of that research: A Unifying Theory of Electronic Money and Payment Systems

Why does Alphabill use bills not UTXOs or accounts?

UTXOs were first proposed by Hal Finney for his Reusable Proof of Work network and subsequently implemented in Bitcoin. In a blog post in 2016, Vitalik Buterin proposed to use accounts as transaction units in Ethereum.

He made the choice of accounts for the following reasons:

• UTXOs are unnecessarily complicated, and the complexity gets even greater in the implementation than in the theory.
• UTXOs are stateless, and so are not well-suited to applications more complex than asset issuance and transfer that are generally stateful, such as various kinds of smart contracts.

These arguments were accurate for blockchains in 2016 when every blockchain was designed to be monolithic with a shared global state. Monolithic here means a single replicated state—all nodes or replicas on the network have the same state. However, the reverse is true when you want to partition state to distribute computation across multiple machines, enabling horizontal scaling.

The choice of accounts implies that every transaction involves two transaction units (the payer and payee accounts), and as the system scales, it leads to cross-machine dependencies for atomic settlement. This leads to the need for Relay Chains (Polkadot), X-Chains (Avalanche), Beacon Chains (Ethereum) in an attempt to manage those cross-machine dependencies.

The same challenges apply to UTXOs. They do allow parallelization within a single machine (that is, you could in theory use multithreading to process UTXOs in parallel). However, UTXOs have multiple inputs and multiple outputs, and if those inputs and outputs are on different machines then the same problem arises—the machines need to coordinate in order to process transactions. This coordination is what limits scalability.

Bills, on the other hand, give the best of both worlds—transaction settlement happens locally on bills and stateful smart contracts execute their code with stateless validation of state (tokens on other machines). They receive certified information about relevant state as inputs and generate new certified information as outputs either for further composition or to be used for settlement.

Bills look similar to UTXOs—what's the difference?

The fundamental difference is that UTXOs are spent not transferred—every transaction involves marking units as spent and creating new units. This makes parallelization difficult and leads to contention issues as a UTXO can only be spent once.

You can think of a bill as a single input multiple output UTXO. Bills are serialized with a unique identifier (leaf address in a Merkle tree) and a transaction order changes ownership of the bill—they are not marked as spent.

A simple analogy would be a highway. Every bill has a lane and will always stay in its lane. You can add more lanes without congestion on the highway. UTXOs jump lanes every transaction.

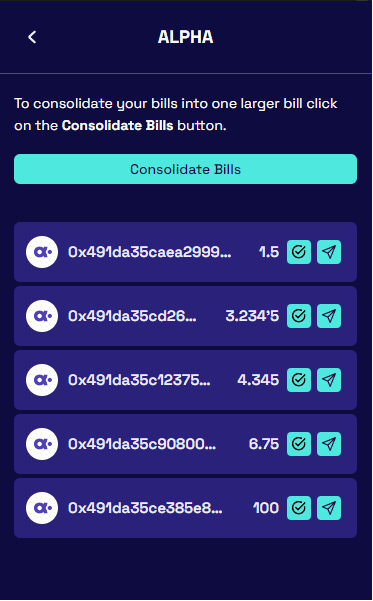
How do you deal with small value units (dust)?

A dust collection process can be initiated by users to consolidate dust bills into a single larger bill (see below). The dust collection is a slower process than regular transfers (it cannot be done in deterministic time and may take several blocks) and out of the critical path.

How would you implement an AMM contract on Alphabill?

In Alphabill, tokens are first-class citizens in the state tree. They exist not as variables in a smart contract, but are allocated a unique address.

In the figure below, tokens live in the token shard and an automated market maker (AMM) contract lives on the contract shard. The mechanism to call a smart contract works without actually moving the token, only the predicate on tokens is changed to allow the smart contract to verify that it is the new owner.

The proof of a token being in the required state is sent to the contract with a subsequent transaction order, that is, the first transaction order is sent by the user to the token shard to lock the token (locking here means that only the specified smart contract can unlock it). A second transaction order is sent by the user to the smart contract shard which includes the transaction request to the smart contract as well as the proof that the token has been locked.

A simplified constant product AMM contract would have two token pools in contract memory, with identifiers (the state tree address) of the tokens locked and sent by liquidity providers.

A user who wishes to swap tokens will send a transaction order to the contract's Swap() function, with locked token proofs as an argument. The contract will then calculate the amount of returned tokens from the pair using the constant product formula, and create unlocking proofs in its memory and terminate. Post block creation, the user obtains a proof that allows them to claim ownership of the returned tokens.

Here is simplified pseudo-code:

function SwapToB(tokensA_in):
     invariant = poolA * poolB        // the product of pool sums is kept constant
     new_poolA = poolA + tokensA_in
     new_poolB = invariant / new_poolA
     outB = poolB - new_poolB          // sum of returned tokens B
     transferTokenBTo(sender, outB)    // creates unlocking proof(s)

The liquidity providers add new tokens to the contract pair-wise in order to maintain the exchange rate. When users see arbitrage opportunities, they can make token swaps, which will bring the exchange rate close to the "real world" exchange rate.

There is no limit to the number of contract calls per round. The advantage of this approach is parallelism and potential "unruggability", meaning that the settlement (change in ownership of tokens) does not happen within the smart contract. Only proofs are generated by the smart contract, which are then sent by users to who can initiate settlement making it possible to introduce a new audit function post smart contract execution.

What's the difference between account and bill sharding?

State, transaction and network sharding become trivial in a bill-based model. Users can maintain a 0 of N trust model by independently verifying only the state they care about.

There are many protocols that have attempted sharding as a mechanism to scale blockchains (Near, MultiverseX, Shardium, Polkadot, etc.). However, account-based sharding introduces the challenge of cross-shard settlement—as the system grows, the probability of a transaction being cross-shard will continue to increase.

In Alphabill, all settlement is local to a bill—there is no need for cross-shard settlement. Alphabill is one big hash tree of assets (bills, tokens or contracts) with different parts of the tree (partitions) operated by sets of machines (validators). All partitions share the same hash tree root enabling stateless verification of state from other partitions.

Cross-shard settlement introduces additional complexity—they require bridges, relay chains, etc., which reduce settlement time with different trust and security assumptions. In particular, users who do not wish to trust the validators are forced to run a node for every shard. Decomposition theory allows us to deliver to users only the state they care about (the tokens they own) and can achieve a 0 of N trust model.

Decentralization and network slicing

The network is sliced into task-specific partitions and that decentralization is addressed individually by assigning necessary quorum sizes for partitions. Can you define what "necessary" means for a given partition?

Please see one of our core papers: A Universal Composition Theory of Blockchains. This document attempts to derive a universal theory to answer this question scientifically. Within the community today we have rules of thumb such as the "blockchain trilemma" or "Nakamoto coefficient". While these can be potentially useful generalizations, they are not based on science. The motivation of the paper is that similar to the draftsman handbooks that you see in civil engineering, it should be possible to derive scientific formula regarding the design for blockchains. For example, how much (fault tolerance, attack tolerance, redundancy, sybil resistance, censorship resistance) do you need? - that's on page X of the Blockchain Design Handbook. We are preparing the paper for publication and believe it will prove to be a significant contribution to the field of distributed systems.

Back to the question. If we assume that user-level token validation is active (that is, recipients of tokens are verifying their histories) and threshold decryption is active (no MEV or censorship), then the answer to "necessary" depends solely on what level of liveness is required. As an example based on independent professional validators, we can expect a liveness of 99.99% for three validators, and 99.999% for five validators.

More generally, it is the number of independent validators to implement the security models of specific partitions, where "security" is addressed more specifically, looking at individual properties, for example, provide sufficient guarantees to satisfy all of certain aspects of security: rejection of invalid transactions, non-forking, and data availability.

We will leave "decentralization" as a subjectively perceived property without formal definition. What we mean by that is that decentralization is not a goal in itself. Instead, it is a tool to achieve the right properties of the system—these properties (data availability, censorship resistance) need to be analyzed individually. See question How decentralized is Alphabill?

What is the source of randomness when it comes to the assignment of validators to partitions and shards?

Alphabill uses the content of Unicity Certificates as the source of distributed, unpredictable, deterministic randomness. This randomness is used for shard leader rotation and also for algorithmic governance processes, including validator assignment. Unicity Certificates are joint statements of the Root Chain validators that certify and prove the uniqueness of the state transitions of all shards in all partitions.

Each Root Chain validator receives summaries of the shard rounds (see the next question) from shard validators. The Root Chain validator then aggregates these inputs to obtain a global summary hash covering all partitions of the system and signs the global summary hash with its private key, obtaining a signature share that derives entropy from both the summary hash (that the validator does not control, as it's computed from the shard summaries in a deterministic manner) and the validator's private key (that the rest of the world can't access).

The signature shares of the individual Root Chain validators are then combined into a joint threshold signature. The combining process is non-malleable (cannot be influenced to have any non-random properties) by individual validators. In particular, each validator has only one chance to produce a vote per Root Chain round, otherwise an equivocation attempt (an attempt to produce multiple conflicting votes) is escalated.

What does the construction of the cryptographic summary provided by the shard validators to the Root Chain validators look like? We're interested in how these summaries are aggregated and efficiently processed.

Presently, the summary (what we call Input Record) contains:

• The state root hash of the previous successful round of the shard.
• The proposed new state root hash (the root hash of the state tree; the state tree has a node for each unit, containing the current state of the unit and the summary hash of its ledger).
• Proposed round number.
• Proposed block hash (the root hash of the tree aggregating all the transactions processed during the round).

• P[j]: transactions of a block
• ι[i]: identifier of a unit; the state tree is a binary search tree indexed by unit identifiers (this ensures a uniquely defined location for a unit's node in the tree and guarantees there can't be two nodes with conflicting states or parallel histories)
• φ[i], D[i]: the owner predicate and state data of a unit
• x[i]: summary hash of a unit ledger

This allows to guarantee certain security properties by enforcing coherent, valid and unique state transitions (for example, show that shard validators can not have hidden parallel states to execute a double-spend attack) relying on fixed-size round summaries from the shard validators.

The implication for efficiency is that the load on the Root Chain validators only depends on the number of shards and the number shard validators, but does not depend at all on the number units managed by the shards or the number of transaction requests processed by the shards.

The data model is not limited to these parameters. For example, partition designers could include a) a compact proof of the correct validation of transactions (SNARK), or b) the necessary data for stateless verification. However, these techniques are currently not implemented in the User Token, Money and EVM partitions as they do not (yet) support our speed-of-finality goals.

What/who governs the Governance Partition?

If a new validator coming onto the network is decided by the Governance Partition, how does the network ensure the governance partition doesn’t censor applicants? What/who governs the governance partition?

The Governance Partition is governed by the ledger rules and ALPHA token holders through on-chain governance. Due to the low transaction volume and long block times (1 minute per block in this partition) low cost consumer hardware can be used to run a validator—we can reasonably expect there to be thousands of validators here. The exact number will be a function of supply and demand, where demand being driven by the percentage of staking rewards that are allocated to this partition. This percentage is in itself the result of a stochastic optimization process.

NB: As of June 2023, the numbers above are still educated guesses—we continue to experiment with the tokenomics.

For the efficiency of the crypto-economic security layer, long-term validator identities are encouraged. Therefore, we have to rely on reasonable decentralization of the Governance Partition to not discriminate against some validators.

Offline payments and double spend

For the offline use case, it is our understanding that the payer locks some tokens for a) a specified period of time, and b) assigns the unlock ability to a certain payee. Once offline, the payer can generate a transfer whose proof is given to the payee and whenever the payee is back online, they can redeem the payment. If for whatever reason the payee cannot come back online after the specified period of time for which the token was locked, do the locked tokens become unlocked to the payer, hence resulting in a double-spend capability?

Offline transactions are an example of a synchronous protocol whose safety depends on timeliness assumptions. Timeouts are a typical measure against permanently locking up funds, and we would expect an application developer who wants to implement offline transfers to enable ownership rollback after a timeout for safety.

The conditions can be adjusted for practical real-world scenarios—the longer the timeout, the more inconvenient it is for the payer. The payer will need to wait for the timeout in order to use the locked cash or receive change from transactions. Too short and the merchant may not have sufficient time to get back online.

Can you walk us through the transaction lifecycle?

It seems as if transaction correctness is provided by a quorum of shard validators, but shard validators don't come to consensus. Can you walk us through the transaction lifecycle?

In the above diagram, we have one client (wallet), a set of three shard validators, and a set of three Root Chain validators. For the purposes of clarity, we will ignore transaction encryption and assume a single leader model.

The client will broadcast a transaction order to the shard validators. The client knows which shard due to the unique address for each unit (bill/token/contract). The transaction order is received by one or more validators and forwarded to the leader for a particular round.

The leader orders the transactions and broadcasts the ordered set of transactions to the other validators in the shard. There is no consensus protocol initiated at this stage.

Each validator in the shard builds its own state tree and generates a cryptographic summary (called input record in the specification—consisting of the state tree hash, round number, hash of previous round, etc.) This is sent to the validators in the Root Chain. (In reality, it is sent to a rotating subset of validators in the Root Chain and then broadcast to the others. At this point, the shard validators do not wait but optimistically start to execute the next round.)

The Root Chain validators receive the cryptographic summaries and forward those to a designated leader. (In reality, there are multiple leaders.) At this point, a low-level consensus protocol is initiated (an Alphabill optimized version of two-round Hotstuff). Note the validators in the Root Chain are not processing transactions—they are simply coming to consensus on the proposed state transitions of the shard validators.

If the Root Chain validators agree that the validators in the shard are in coherence—there is timely majority agreement that extends previous certified state, etc.—they will issue a Uniqueness Certificate (a BLS signature of the Root Chain validators) and return that independently to each validator in the shard.

The shard validators will independently check the consistency of the Uniqueness Certificate, add the Uniqueness Certificate to their blocks, and then start the next round of validating transactions. (The diagram shows a single validator returning the Uniqueness Certificate. In reality, it is a subset of Root Chain validators not just one.)

How do you manage shared ownership of assets?

Shared ownership of assets is managed through predicates (locking scripts) on individual tokens. For example, a predicate might encode a condition saying "next transaction order must be signed by public key A OR B", giving shared ownership of the asset. Another example would be a condition saying "next transaction order must be signed by public keys A AND B" giving multisig semantics to ownership. If there are multiple concurrent transaction orders, they are ordered by shard validators managing this token. This happens locally within a shard without requiring global ordering.

How does Alphabill ensure data availability?

Data availability is an issue for blockchains that support stateless validation: validators do not have to synchronize the blocks and therefore maintain a replica of the blockchain. Instead, they rely on compact proof of the transacting unit's current state in order to validate a proposed state transfer. Another example where extra effort is needed for availability is L2 rollups; solved via data availability layer or by simply posting transaction data back to L1. The Polkadot Relay Chain is another example of stateless validation where a separate data availability protocol is necessary.

In Alphabill, everything is on-chain and there are sufficient partition quorum sizes to ensure that copies of historical transactions are always available.

In addition, the parallelism of Alphabill ensures that each unit (token or contract) can be downloaded, verified and saved locally by users to guarantee availability of the asset transaction histories.

This is similar to physical cash—you can verify the availability of your physical cash because it is inside your own wallet.

What is the difference between state and transaction proofs?

The figure below shows the evolution of the state tree over time. Each leaf of the tree represents the state of a unit (token or contract). The blue hash values show how the state tree is built recursively, in that each blue hash value is a hash of the combination of the state of the unit and the last transaction with this unit. The blue hash value does not change if there are no transactions.

A unit state proof is a proof that a specific unit has a certain state at the proof generation time and that it is the result of executing a specific transaction. Alternatively, a unit state proof can prove the non-existence of a certain unit. A transaction proof confirms that a transaction was executed during a certain round.

How do I write smart contracts in Alphabill?

Alphabill does not use proprietary languages for smart contracts. It is possible to have different smart contract partition types implementing different smart contract platforms, including Ethereum's EVM, WASM, DAML, Hyperledger, etc. There are no restrictions and each smart contract interact with smart contracts on other shards using the shared Root Chain certification.

Initially, the first smart contract platform implemented is the Ethereum EVM.

How do fees work in Alphabill?

Alphabill’s gas pricing mechanism guarantees low, predictable transaction fees for users, incentivizes validators to perform their transaction processing operations, and prevents denial of service attacks.

A key design goal of Alphabill is Zero Extractable Value, meaning that validators are economically incentivized to participate in processing transactions, but have no agency to decide the price, order, or number of transactions to be processed. As such, the gas price is determined by a decentralized governance process to ensure fees remain as low as possible, with the constraint that there are sufficient incentives to ensure an optimal number and diversity of validators to participate in the network.

Due to parallelism inherent in the Alphabill network, we can guarantee, apart from short-term spikes, that long-term supply can always match demand. Throughput scales linearly and as demand increases, the network can add more machines, operating in parallel to process transactions.

How does checkpointing work in Alphabill?

Alphabill is a single global state tree which evolves over time. The root hash values are recorded in a data structure whose root is periodically recorded in the Unicity Trust Base (see the next question) as a checkpoint. This mitigates long-range attacks.

How do you do offline transactions?

Alphabill supports transfer of assets with final, irrevocable payments even in the absence of network connectivity. In our approach, a system of predicates is used to control access to different actions on individual assets. Predicates are simply functions that accept a number of arguments and return true or false. The predicate that controls ownership is the "owner predicate".

For example, a "transfer" transaction supplies arguments to the current owner predicate and contains a new owner predicate, which is to be installed upon success, meaning that if the arguments result in the function returning true, then that transaction succeeds, and the new owner predicate replaces the old one. A predicate can only be replaced, not modified.

A payer who wishes to transfer bills offline to a known payee (for example, a subway operator) can assign a predicate that "locks" the bill and can then be unlocked either a) after a specified period of time (for example, one week) by an arbitrary transaction from the payer, or b) by a transaction order from the payer, where the recipient can only be the known payee. In an environment with no network connectivity, the payer can then generate a transaction order for a specified amount for the payee and digitally transfer the transaction order without network connectivity to the payee, who can independently and with mathematical certainty verify that only they can unlock the bill and claim ownership prior to the timeout period. Once the payee has connectivity, the payee will send the received transaction order to the settlement service and claim unconditional ownership of the bills.

How do you do off-chain verification?

In Alphabill, it is possible to mint tokens on-chain and verify them off-chain or even offline. To achieve this off-chain verification, a verifier needs three things: the data, a proof, and the root of trust.

• Data to be verified is typically the unit state.
• Proof is a unit (token or contract) state proof or transaction proof. A state proof proves that a unit is in a certain state (for example, who is the owner of a token, or the value of a variable in a smart contract). A transaction proof proves the execution of a specific transaction (for example, Alice transferred a token to Bob).
• The root of trust is a compact data structure called the Unicity Trust Base, consisting of the genesis block providing initial system parameters, the public keys of the Root Chain validators and the security checkpoints. The Unicity Trust Base evolves over time based on a decentralized governance process as the Root Chain validator set changes.

How do you prevent double spending in Alphabill?

Double spending is impossible by design in the Alphabill model. Each token has a unique address in the state tree and there can only be one proof of uniqueness per transaction per block, assuming the hash function used is collision-resistant. The proof of uniqueness is generated by the Root Chain validators, which do not validate individual transactions directly and generate a Unicity Certificate which is used to ensure partition validators cannot sign alternative histories.

What are the tradeoffs in Alphabill—what can it not do?

Anything that requires a shared global state. For example, flash loans would be impossible in Alphabill.

Security

How does a token ledger's validity get efficiently determined by users for it to be a practical layer of security?

In this answer, we are going to walk you through the verification of a unit ledger (note that we use "unit ledger" here as opposed to "token ledger" as it can represent any asset, including bills, tokens, and contracts).

When it comes to scaling, almost everyone in the community thinks about scaling of production (how many TPS), but scaling of verification is as important. In this context, decomposition theory ensures that the global ledger can be subdivided into subledgers (unit ledgers) such that verification of the ledger can be parallelized. Volunteers can be allocated parts of the ledger at random and can receive audit rewards (allocated as a percentage of staking rewards) in order to check the consistency of the ledger in real time. This process can be automated and cryptographically verified.

• P[i]: records of transactions manipulating the unit
• t[i]: hash of P[i]
• x[i]: summary hash of the unit ledger up to (and including) P[i]
• φ[i], D[i]: the owner predicate and state data of the unit after executing P[i]
• Cunit[i], Ctree[i]: Merkle tree certificates linking the unit's identity and state to UC[i]
• UC[i]: Unicity Certificate for the round in which the partition processed P[i]
• V[i]: summary value of the state tree subtree rooted at the node for the current unit (for verifying the total value represented by the state tree and thus maintaining the money invariant, or ZK proof if applicable).

In short, unpermissioned RPC nodes (similar to validators except they do not have an active role in consensus, but instead solely provide data access services to end clients) provide an API which returns unit ledgers to end users. RPC nodes are not required to be trusted—they simply extract the unit ledgers from the shard's global ledger and forward them to clients. Client-side libraries then verify the unit ledgers, based on an independent root of trust (see question How do you do off-chain verification?)

After obtaining the unit ledger, the client can independently verify that:

• Each transaction is valid given the unit's previous state.
• Each new state of the unit is what it should be with the latest transaction applied to the previous state.
• The transactions form an unbroken hash-linked chain.
• Each new state links (through the two Merkle tree certificates) to a valid Unicity Certificate (UC) issued by the Root Chain.

This is very efficient, as the number of entries in the unit's ledger is the number of transactions with the unit and does not depend on or need to reference transactions or states of other units. Also the Merkle tree certificates are small: Cunit[i] is logarithmic in the number of transactions with the unit within the same round where P[i] was processed (which is just 1 for majority of transactions with bills and tokens) and Ctree[i] is logarithmic in the number of units managed by the partition, for a total of about 30 entries of a few tens of bytes each in a partition with a billion tokens and about 40 entries in a partition with a trillion tokens.

There are two additional pieces of functionality that we are developing:

1. ZK Compression

Decomposition theory ensures that each unit has an independent history. We can potentially compress that history with ZK techniques such that a client, instead of going through the history of a unit and verifying each transaction, can simply verify a ZK proof. The idea is that periodically the validators or users will generate a recursive ZK proof certifying the correct transaction history and store that in the unit ledger ensuring efficient unit ledger verification regardless of the number of previous transactions.

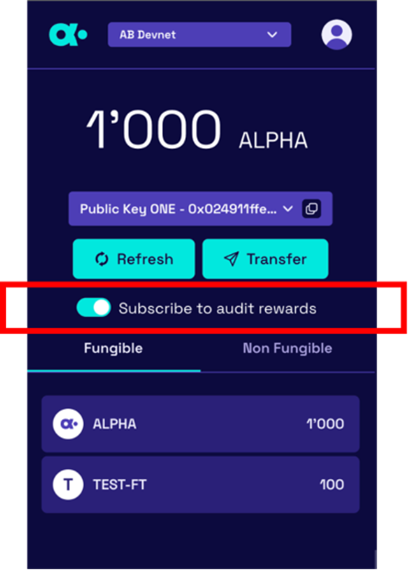
2. Crowdsourced auditing

See the red box below. Users can subscribe to audit rewards and volunteer to participate in the verifying of unit ledgers. In other words, the system can adjust the allocation of staking rewards to ensure that unit ledgers are independently verified immediately after block creation by a specified number of independent auditors.

How decentralized is Alphabill?

We will give a general answer and then a longer, more precise answer.

General answer

Quoting Vitalik from his blog post on scaling blockchains while maintaining decentralization.

"For a blockchain to be decentralized, it's crucially important for regular users to be able to run a node, and to have a culture where running nodes is a common activity."

Vitalik is the pioneer who came up with the concept of decentralized compute, but there was no theory in 2016—he didn't have decomposition theory to guide him.

With Alphabill, due to parallel decomposition, we can change this statement to "For a blockchain to be decentralized, it's crucially important for regular users to be able to independently verify their assets, and to have a culture where verifying assets is a common activity."

The analogy with physical cash is relevant. When I give you a 20 USD note, you just check the validity of that note. You don't need to run the entire economy on your mobile device and check every other transaction in history to be sure that your 20 USD note is valid. (NB: The absurdity of this statement is, in our view, the reason there is limited real-world adoption of crypto.)

One way to scale blockchains is centralization, such as Solana and SUI with high-powered computers as nodes (one shardable, the other not). Another way is decomposition, that is, efficient independent verification of assets. In a sense, this is in line with Vitalik's vision except that the work of a "node" can be divided into verifying tokens which can be done by the crowd in real time.

Longer answer

Decentralization is a compromise. More decentralization adds overhead as there are more replica machines that synchronize the state and re-do the same computations to validate state changes, in order to overwhelmingly outbalance the effect of a malicious entity trying to obstruct or overtake the network.

Alphabill achieves efficiency by providing redundancy in a flexible way.

Firstly, the abstract concept of security is decomposed into its sub-components, addressed by a sufficient amount of validation resources.

Secondly, the network is sliced into task-specific partitions; decentralization is addressed individually by assigning necessary quorum sizes for partitions. This allows having partitions with a very high level of decentralization (for example, the governance and native currency partitions) or running with just a few validators (such as enterprise application partition).

• The most important aspect of security is the property of safety. This includes non-forking at unit level (no double-spending) and at partition level (no alternative hidden histories of partitions). In order to fork, an attacker must control a configurable number between 51% and 100% of partition validators AND at least 2/3 of Root Chain validators, that is, Root Chain is offering "shared security" to partitions.

• The property of validity (rejecting invalid transactions) is guaranteed by a configurable number between 51% and 100% of partition validators.

• The property of not breaking liveness is guaranteed by between 49% to 0% of partition validators (inverse to previous) OR at least 1/3 of the Root Chain validators.

• Censorship resistance and fair ordering (MEV prevention) are provided by the user's option of sending transactions to any number of validators, rotating the leaders proposing blocks, and "mempool encryption" where transactions are threshold-decrypted after ordering.

• Confidentiality of transactions is a property of some partitions, such as "dark partition" and using zero-knowledge tools.

• Data availability of transactions is provided by a quorum of partition validators.

It is also important to consider the effect of an attack by the aspects of security—whether it is detectable, recoverable or can potentially stay unnoticed. The existence of a parallel history is hard to detect, thus has a more severe effect than, for example, validating transactions not according to the ledger rules.

On top of the security offered by just quorum sizes, it is necessary to note that validators are assigned to partitions and shards unpredictably and then shuffled periodically, which makes the cost of gaining majority in a specific shard much higher.

There is also a crypto-economic security layer—staking and incentive mechanisms make it non-economical for a single well-resourced attacker to try anything bad. Quorum size requirement and crypto-economic security together protect against irrationally behaving extremists.

Eventually, when the progress in Zero Knowledge technology starts to support our settlement time goals, it is possible to submit succinct proofs of correct operation from shards to the Root Chain, dramatically reducing the sizes of shard validator quorums while maintaining sufficient security.

Do users need to trust the Alphabill validators?

In Alphabill, users have a choice. They can choose to trust an honest majority of validators in the network and verify only using unit state proofs or transaction proofs. In order to exclude trust in validators, users can choose to download and verify unit ledgers which can be verified without any trust assumptions. Unit ledgers include only the historical transactions of that unit, and their sizes will be many orders of magnitude smaller than conventional blockchains. "Full client" security and auditability is provided without the overhead of non-related transactions.

In the context of money, this is similar to the physical cash in the real world. When someone gives you a 10-dollar bill, you don't care about every other bill in the economy, only the one you receive.

What is the Alphabill Trust and Security Model?

The parallelism of Alphabill allows for different trust models to be selected by users. Every user is able to independently audit the individual token histories that they have ownership of. They can store not just the private key that controls transfer of the token but also the token ledger itself. This is similar to physical cash—a consumer cares only about the verifiability of the cash that is inside their wallet, not that of everyone else in the economy. This independent verification at the token level opens up new methods to ensure data availability and detection of malicious activity.

There are effectively five layers of security to detect and mitigate malicious behavior.

• The first layer happens during the block production process. Validators on a shard independently send a cryptographic summary of their transactions to the set of Root Validators. On a partition level basis, the required level of agreement between the Transaction Validators can be selected through a partition management governance process to determine the level of safety vs. liveness for the partition in question. This layer guarantees security on the assumption that up to a certain ratio of candidate validators are malicious.

• The second layer also happens during the block production process. A single honest validator that is part of the validator set within a shard can detect malicious activity through the validation of transactions. If malicious activity is detected, a fraud proof can be generated and sent to the Root Chain prior to the Unicity Certificate being created and returned to the shard. This layer guarantees security on the assumption that there is at least one non-colluding validator observing the invalid block proposal. There is no restriction on the number of validators in a shard, and the settlement time is not impacted as the number increases. Hidden, or observer validators, can join a shard and participate in securing the network.

• The third layer is crypto-economic security. Here, the underlying assumption is that validators are potentially malicious, but economically rational actors. The cost of losing rewards and potential slashing outweighs the economic gain of malicious activity. It is still possible that a malicious actor behaves irrationally, for example for fame, but it is very unlikely that a majority of validators behave in self-sacrificing way.

• The fourth layer of security is applied post block production. Here, the underlying assumption is that all validators in a shard are malicious, adaptively collude and hidden validators have not detected malicious transactions. Users can earn "audit rewards" by volunteering to participate in a crowd-sourced verification of the ledger by sharing the work of auditing every block in every shard in every partition. The work is split up among the volunteering pool of wallets using a random sortition process. If an inconsistent block is discovered, a fraud resolution process is initiated with potential slashing of offending validators. This function has the additional benefit of verifying data availability of the ledger.

• The fifth layer of security relies on users to verify the history of each individual token that they take ownership of. In Alphabill, due to the decomposition function, a user can do this independent verification at the token level, that is, users do not need to rely on validator-cluster generated proofs but can instead verify compact token ledgers. In other words, a recipient of a token can verify that a) the token was minted in a valid genesis event and b) all historic transactions associated with that token have been executed correctly.

In the original Bitcoin blockchain, there is no requirement for users to trust anyone. A user can download the entire blockchain, go through the ledger transaction by transaction to independently verify its consistency. However, as the system scales, this approach inevitably leads to centralization. For example, at 1 million transactions per second the Bitcoin blockchain would be in the order of 1 exabyte of data, making it beyond reach of individual users to conduct independent verification. In Alphabill, due to the decomposition function, a user can do this independent verification at the token level.

How does Alphabill provide global ordering of transactions while maintaining efficiency?

Global ordering is not needed in Alphabill. There is ordering within each shard, so that each validator ends up with exactly the same sequence of identical blocks. Transactions targeting different units can be executed in any order as the final state does not depend on it. But if there are many transactions targeting one unit, executed within one round, then the transactions are likely not commutative and the final result depends on the execution order. Thus, transactions modifying one unit within one round must be executed by strict order.

Alphabill is an open platform for creating heterogeneous partitions. The generic transaction system (base partition type used to create specific partition types) does not have rules about ordering of transactions. Specific partition types usually have, either explicitly or as a byproduct of transaction, replay protection. There are two replay protection mechanisms in use: backlink (a valid transaction must include the hash of previous transaction targeting the same unit), or nonce (a unique number). The backlink or nonce is specified by the user who creates a transaction order, and verified by validators. For example, Money Partition type has strictly increasing nonce requirement, whereas data integrity partition does not (transactions there are idempotent), whereas smart contract partition, where anyone can call a contract, has replay protection and ordering separated. Only on the latter case it is up to validators to decide the transaction ordering.

Indeed, there are certain similarities with Sui: for single-owner units, the ordering matters only for packaging transactions into blocks, and if there are many transactions per block, then the owners specify the ordering. For sharded units, there must be shard-local ordering, provided by validators. Providing shard-local ordering is easier than providing global ordering. The relative ordering of blocks of different shards and partitions is in fact recorded: the root hashes are aggregated into a globally shared Unicity Tree data structure by the Root Chain. Relation can be "the same" when blocks are certified by the same Root Chain round.

Principally, shards only validate transactions, there are no extra protocol steps to achieve consensus about ordering. Root Chain certifies only requests which are in agreement, thus, the agreement on ordering comes almost for free.

How does Alphabill cope with the fundamental theorems of database systems?

CAP theorem

CAP theorem states that any distributed data store can provide only two of the following three guarantees:

• Consistency: every read receives the most recent write or an error.

• Availability: every request receives a (non-error) response, without the guarantee that it contains the most recent write.

• Partition tolerance: the system continues to operate despite an arbitrary number of messages being dropped (or delayed) by the network between nodes.

The protocol rules of Alphabill guarantee safety at all times (assuming no arbitrary behavior due to Byzantine majority). Liveness is guaranteed only on the participation of sufficient quorums of validators. If the system gets partitioned, then a certain ratio of validators is excluded from forming the quorums. Thus, if large enough chunk of the validators is separated from the rest, there might be not enough validators left to form unique quorums and the system stops, sacrificing liveness to guarantee safety. The system may reconfigure if a quorum of the Governance partition is alive and can continue operation with different sets of validators in other partitions.

CAP theorem interpretation depends on the viewpoint.

If we consider a blockchain replica (maintained by an RPC node, for example) as the interface, then Alphabill guarantees availability and partition tolerance, but no consistency as the replica may be temporarily missing some last blocks. This is eventual consistency.

From a validator's viewpoint, the protocol guarantees consistency and availability, but not partition tolerance—it is not possible to participate in the protocol if a validator is separated from the majority and out of synchronization.

ACID

ACID is a set of properties of database transactions intended to guarantee data validity despite failures.

• Atomicity guarantees that a composite transaction is either executed fully, or not executed at all.

• Consistency guarantees that a database is updated only according to the database rules, which in the blockchain case are the validation rules.

• Isolation means that concurrent transactions do not interfere with each other, the effect is the same as if they were being executed sequentially.

• Durability guarantees that once a transaction is committed, it remains to be committed no matter of future failures.

Alphabill guarantees all these transaction properties, given underlying security assumptions are met. Different unit's updates are isolated due to the bill model; thus, their relative ordering does not matter. Atomicity relies on the Atomicity partition.

PIE theorem

PIE theorem: pick only 2 from Pattern Flexibility (support of unexpected queries), Efficiency, Infinite Scale.

Alphabill is not a database, its output is finalized blocks. The stream of blocks is not an efficient nor flexible query interface. For flexible queries, it is necessary to include middleware components like "indexer" or light wallet backend. These services have database properties, thus all specific limitations, including the PIE theorem, apply.

PACELC theorem

PACELC theorem states that in case of network partitioning (P) in a distributed computer system, one has to choose between availability (A) and consistency (C) (as per the CAP theorem), but else (E), even when the system is running normally in the absence of partitions, one has to choose between latency (L) and consistency (C).

Alphabill side-steps the extra constraints of the PACELC theorem by employing the bill-based model, which allows to shard the system without guaranteeing consistency between shards, while well-dimensioned shards provide acceptable latency.

How does Alphabill deal with the blockchain trilemma?

The blockchain trilemma, as termed by Vitalik Buterin, refers to a widely held belief that decentralized networks can only provide two of three benefits at any given time with respect to decentralization, security, and scalability, where security was defined as the chain's resistance to a large percentage of validators trying to attack it.

The challenge with this approach is that "security" is too broad and needs to be defined through its individual aspects—forking resistance, censorship resistance, double-spending prevention, data availability, rejecting invalid transactions, etc. See question How does Alphabill cope with the fundamental theorems of database systems? for a summary of a comparison of Alphabill against scientific claims that can be quantified and measured, such as CAP, ACID, etc.

In Vitalik's blog post, he references High-TPS chains:

High-TPS chains - including the DPoS family but also many others. These rely on a small number of nodes (often 10-100) maintaining consensus among themselves, with users having to trust a majority of these nodes. This is scalable and secure (using the definitions above), but it is not decentralized.

In the case of Alphabill, due to the native parallelism users do not need to trust a majority of validators and can do the independent verification of the assets that they own.

Major aspects of security are provided by the Root Chain due to the shards presenting compact proofs of correct state transfers, including hard-to-detect ones like parallel states and forking attacks. Due to the sheer amount of transaction data, the correctness of individual transaction validation is provided by quorums of shard validators, in the anticipation that succinct cryptographic correctness proofs of execution (for example, SNARKs) become viable in the near future.

How does Alphabill mitigate PoS attack vectors?

Long Range attack

Long Range attacks attempt to undermine Proof of Stake consensus blockchains by abusing validator private keys of a certain epoch at a later point in time when the validators have already received their fees. For example, they can create alternative versions of historic blocks where transactions look valid.

In Alphabill, users can rely on unit ledgers which makes forking of bills detectable. In addition, there is a checkpointing mechanism where the summary hash of historic state trees is stored in the Unicity Trust Base.

Grinding attack

Grinding attacks happen when malicious validators attempt to subvert the validator and block-leader election process to gain more rewards or execute double-spending. In Alphabill partitions, the leader election process happens based on non-malleable randomness provided by the Root Chain. Validator assignment to partitions and shards is covered by a decentralized governance process.

Nothing-at-stake attack

A nothing-at-stake attack happens when validators are incentivized to stake and validate multiple parallel chains in order to receive more rewards. In Alphabill, staking in parallel forks is punished with slashing. Staking in multiple partitions is acceptable behavior.

Alphabill Comparisons

How does Alphabill compare to traditional database systems?

Short answer

To make a sensible comparison, the database solution should be doing something similar to Alphabill—running a distributed transaction system with signature verification, verified finality and consistency across multiple replicas. Alphabill assumes a far stronger threat model than, say, NoSql databases such as Apache Cassandra, which has similar scaling asymptotics and similar latency (single second finality).

Longer answer

Alphabill is a permissionless distributed ledger. It assumes a far stronger threat model, at the cost of certain rigidity at the user interface layer and reduced efficiency due to decentralization-induced redundancy.

Some of the things Alphabill can do:

• Output a cryptographically secured replica (blockchain), where data integrity is guaranteed at the data layer, verifiable by anyone. Untrusted party can run a query interface, so that results (proofs) are individually secured, and can be further passed on.

• Operate in an adversarial environment where no insiders or outsiders can be trusted.

• Recover from a wide range of attacks, and scale automatically without privileged parties' support.

• Provide a non-tamperable append-only transaction log.

• Have undeniable finality (incurring some latency overhead).

• Programmability (predicates and smart contracts vs. stored procedures).

• Cross-shard atomic transactions.

• Partitions with heterogeneous use cases.

Alphabill's ledgers are not a convenient query interface. There is a middleware layer with "RPC Nodes" and "blockchain indexers" offering developer-friendly interfaces, while retaining the security benefits mentioned above.

Alphabill, whose shard validators re-validate all transactions in a shard, is more efficient than traditional blockchains whose performance is bounded by a single machine and transactions re-validated by everybody. On the other hand, in database systems usually one machine executes all transactions, and the relaxed trust model does not require re-validation. Without sharding, this machine is also the performance bottleneck, as in a high-availability cluster there is only one read-write machine and many read-only replicas. Distributed NoSQL databases (such as Apache Cassandra) use a key space that is distributed across a ring of equal servers. Due to data cross-replication, the consistency is not guaranteed. Just like in Alphabill, a query can return data from a single partition.

Alphabill is not designed for bulk data storage, which can be offloaded to, for example, IPFS and only summary hash is maintained by Alphabill.

How does Alphabill compare to Polkadot?

The Polkadot team made a significant contribution to the blockchain community by pioneering the concept of sharding and shared security. Polkadot has shards (parachains) each of which is a sovereign blockchain (the parachains may be permissioned, permissionless, have a sovereign token…). The network uses a shared security model—a separate blockchain, the Relay Chain, governs the parachains. The shared security model ensures that a subset of randomly assigned validators (typically 3-5) in the Relay Chain check the state transition proofs of the validators in the parachains. The Relay Chain also passes messages using the XCM messaging protocol across parachains to facilitate cross-shard settlement. The Relay Chain uses accounts as transaction units. Polkadot is based on the longest chain rule for consensus along with a "finality gadget" which provides settlement finality within 60 seconds.

The foundational difference is that Alphabill uses bills as transaction units. That means all assets (tokens, contracts) are independent, there is no need for global ordering and all settlement is local—it is possible to validate transactions based on local information only, that is, based on token state and transaction order alone. There are no other data dependencies. The implication is that cross-shard settlement is not necessary as value never moves—only ownership of value changes.

Alphabill has a shared security model loosely similar to Polkadot. A major difference is that the Alphabill Root Chain does not validate transactions. Validators in shards send cryptographic summaries of a proposed state transitions to ALL the validators in the Root Chain, which then come to consensus about uniformity and validity, and then certify the state transfers with a proof of uniqueness. The validators in a shard do not come to consensus—they are independent worker machines that update ownership of tokens. As such, deterministic finality can be achieved across all shards within one block. The Root Chain Unicity Certificate is present in all committed shard blocks. Thus, it is possible to extract a compact proof about the individual state of a single token, and this is immediately verifiable by all shards/partitions and external entities having the authentic root of trust (Unicity Certificate) of the Root Chain.

The other major difference the bill model provides is parallel verification of token state. As assets are independent, it is possible to extract a token, verify it, and act upon with a vastly reduced amount of information.

This is achieved through a concept called state tree recursion. The tokens are first-class citizens in that they are not variables inside a smart contract. They are allocated their own state space and recursively linked together as shown in the diagram above—the blue dots are the block headers for a blockchain for an individual token (a unit ledger).

How does Alphabill compare to Avalanche?

The Avalanche team have made important contributions to the field including a new "Snow" family of consensus protocols which use randomized sub-sampled voting and Directed Acyclic Graph data structures to achieve fast probabilistic finality.

The Avalanche design is based on a heterogeneous network of many blockchains, each of which has a separate set of validators and consensus instance. The three main chains are: a) the P-Chain, or platform chain which acts as a governance layer for the creation of other blockchains, b) the X-Chain which is a UTXO-based asset chain using a DAG (Directed Acyclic Graph), and c) the C-Chain which is an EVM compatible smart contract chain. Developers can create sovereign blockchains, or subnets, through the P-chain.

Alphabill is a different design targeting a different set of use cases.

In Alphabill, there is a single blockchain with a single consensus instance across the network. The use of bills as transaction unit and state tree recursion ensure that the chain is perfectly parallelizable—all settlement is local, and all assets can be updated and verified in parallel. This is the basis for linear scalability (practical unlimited throughput).

Deterministic finality (no re-orgs) is a requirement in Alphabill as certificates (proof of uniqueness, proof of transaction, proof of unit existence, proof of unit non-existence) are created on-chain and potentially used off-chain. A re-org, as it can appear in Avalanche, would invalidate a certificate issued during the re-org which would be problematic for external users relying on a certificate.

Avalanche distinguishes between local and total ordering. The X-chain is used for simple or composite transfers of assets, such as AVAX (the assets are based on UTXOs stored in a database similar to Bitcoin) and the C-chain or subnets can be used for applications that require a total ordering.

In Alphabill, all settlement is local and total ordering is not necessary as there are no interdependencies to track. To achieve this, a state tree is built and a change in state (settlement) happens locally for each asset. The state tree is global and provides a common framework of reference so that all assets are verifiable without synchronization across shards.

In traditional blockchains, assets are created as variables inside smart contracts. In Alphabill, contracts are separate from the assets. They receive state proofs as inputs and generate proofs as outputs, which can then be used to initiate settlement. In other words, value doesn't move, only ownership of value changes.

How does Alphabill compare to Cardano?

The Cardano team have been pioneering blockchain technology for almost 10 years. They developed the Ouroboros Proof of Stake protocol and their focus on formal methods and peer-reviewed research sets the standard for protocol development.

Cardano is a single partition architecture that uses UTXOs as transaction units. The goal of Alphabill is to build a multi-partition architecture where many partitions process transactions in parallel and each asset created on-chain can be independently verified off-chain or even offline.

To achieve scale through partitioning, it is challenging to use UTXOs as UTXOs may have multiple inputs and multiple outputs which may exist on different partitions. If the UTXO set is sharded (they are split into subsets which live on different partitions), then the machines in different partitions need to coordinate during transaction execution in order to ensure ledger consistency. This ultimately breaks the parallelism and limits scalability.

In this regard, UTXOs are similar to accounts in that transactions will always involve more than one transaction unit. This is not the case for bills, which involve only one transaction unit during transactions.

In Alphabill, we relax this constraint and allow for more than one output, but we can guarantee, due to the data model design, that the output transactions will always be in the same partition ensuring parallelism is not broken. Due to strictly scoped validation context, Alphabill can execute many transactions with a single bill during one round.

The implementation is through a Merkle tree—the bills (native Alphabill currency) or user-created tokens are uniquely identified through the address on the Merkle tree.

There is one other major advantage of using bills over UTXOs. The Cardano data model leads to significant contention challenges when implementing smart contracts, for example when multiple people attempt to access the same UTXO at the same time. This is not the case for bills or Alphabill smart contracts.

Smart contracts in Cardano are implemented using extended UTXOs or EUTXOs, which support scripts and arbitrary data. The approach has advantages over the shared state approach; however, it requires developers to have an understanding of the concurrency tradeoffs in the design process.

In Alphabill, we take a different approach. Similar to EUTXOs tokens (which exist as first-class citizens on the state tree) support "predicates" or scripts which can "unlock" tokens; however, it is possible to implement smart contracts using partitions which implement general purpose smart contract development platforms such as Solidity.

The first step is to transfer conditional ownership of a token to a smart contract. This is done using predicates, where a user sends a transaction order to a token address assigning ownership to a smart contract, together with a timeout period so that if the contract fails, ownership is reverted back to the original owner. Once the new predicate has been registered in the token ledger, the data and proof can be sent to the smart contract address. As the smart contract and token share a common unicity framework, the smart contract can verify the correctness of the proof of the token transfer and execute its code accordingly. The smart contract then generates proofs which can be used in further composition or transaction settlement.

This approach combines the best of both worlds—there is no shared state among contracts, and developers have the flexibility to use any development environment. Alphabill has its own EVM-based development environment, but any run time can be used, including Ethereum, provided the environment has access to the Unicity Certificate generated by the Root Chain in order to verify the proofs it receives as inputs.

How does Alphabill compare to layer 2 scaling solutions?

Layer 2 solutions are proposed as solutions to the scalability limits of layer 1 protocols. However, these either sacrifice security (Optimistic Rollups) or performance (ZK Rollups). Due to the state commitments in layer 1, they improve throughput by using centralized components, before hitting a hard limit due to the amount of information which has to be posted back to layer 1. There is also no direct way to settle transactions across rollups, whether that is a simple payment or linking smart contracts together (composability). Another challenge for rollups is censorship resistance—they are typically single monolithic servers.

Alphabill does not require layer 2s, sidechains or any type of off-chain scaling solutions. Scaling happens on-chain.

How does Alphabill compare to the Internet Computer (IC)?

The IC is designed by a team of world-class cryptographers and computer scientists who have made numerous contributions to the state of the art, including chain-key cryptography, reverse gas and a governance DAO to ensure decentralized governance of network operations. The goal of the IC is to be a platform for decentralized applications as an alternative to the traditional centralized cloud providers such as AWS.

Alphabill has a completely different design, purpose and set of use cases. The two platforms are compatible in that a developer can mint tokens on the Alphabill platform and use those tokens in applications built on the IC.

The IC uses a federated blockchain approach where each subnet has a separate consensus instance with a distinct set of validators that come to consensus for that subnet. Each subnet is secured separately. Cross-application communication is achieved through message passing of certified state, certified using chain-key cryptography, that is, threshold signatures are used to certify the state in one subnet and a single public key can be used to verify that state on applications in other subnets.

Alphabill takes a different approach—the goal is to build a massively parallel state machine, that is, it is a single state tree where all assets (tokens, contracts) exist on the state tree and can be updated and verified in parallel. There are no interdependencies between assets and assets can be minted on-chain and then verified off-chain in other applications, including IC canisters. It is not possible to have multiple parallel copies (forking) of subtrees representing partitions. Such guarantees cannot be provided by public-key signatures alone. In other words, there are no cryptographic guarantees of uniqueness of subnet states.

The Root Chain Unicity Certificate is present in all committed shard blocks; thus, it is possible to extract a compact proof of uniqueness about the individual state of a single token, and this is immediately verifiable by all shards/partitions and external entities having the authentic root of trust (see question How do you do off-chain verification?).

How does Alphabill compare to Sui?

Both Alphabill and Sui use simplifications enabled by the reduced dependencies between objects. For Alphabill, there are no dependencies at all. All assets are independent of each other and can be updated and verified in parallel.

In Sui, objects can either be shared or non-shared. A simple asset transfer would be an example of state change for a non-shared object which can be implemented without global consensus—it can be reduced to a reliable broadcast protocol with involvement of the object owner.

1. The sender (object owner) broadcasts a transaction to all Sui validators ("authorities").

2. Each Sui validator replies with an individual vote for this transaction. Each vote has a certain weight based on the validator's stake.

3. The sender collects a Byzantine-resistant-majority of these votes into a certificate and broadcasts that back to all Sui validators. This settles the transaction, ensuring finality: the transaction will not be dropped (revoked).

For Sui, the execution order of single-owner objects is provided by the object owners. In Alphabill, the state tree is sliced into manageable shards, where execution order is provided by shard validators. There is no need for global ordering of transactions.

Sui's shared objects go through a global full consensus before settlement. To deal with the cross-dependencies of shared objects, Sui introduces the MOVE language which is designed with safety features to manage the dependencies and simplify the developer experience. In Alphabill, there are no dependencies at all so there is no need for specialized programming languages to manage them.

How does Alphabill compare to Modular blockchains?

The term "modular blockchain" appears in the marketing of Fuel and Celestia. The idea is that the functions of the blockchain (execution, settlement, data availability and consensus) are provided by separate sovereign networks which are plugged together to provide a fully functional blockchain.

Alphabill is modular in the sense that the functions of the network are decomposed into partitions which provide execution and availability and the Root Chain which provides consensus support and orchestration.

Alphabill differs from the modular blockchain approach in that it is fully parallelizable.

Transaction validation and verification can be decomposed and executed by many machines in parallel.